one way ANOVA,
1. 귀무가설(H0) : 모집단에서 모든 group의 평균은 같다. 즉 그룹간에 차이가 없다.
대립가설(H1) : 모집단에서 모든 group의 평균은 차이가 있다.
2. 가정
- 각 group들은 모두 독립적이어야 한다.
- 각 group의 sample size가 서로 같거나, 비슷해야한다.
- 모수적 검증이기 때문에 정규성을 만족해야만 한다.(sample size>30)
- 모집단에서 group들의 분산이 같다는 등분산 조건을 만족해야만 한다.
(Leveno's test 실시 or Bartlett test 실시)
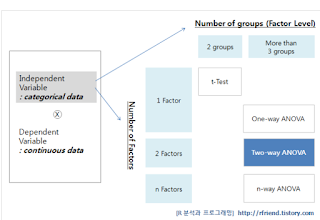 그림1
그림1위그림과 같이 anova 분석은종류(factor(요인), group(factor level, 요인수준))에 따라서나뉜다.


분산분석은 측정된 자료값들의 전체 변동을 비교하자 하는 요인수준(factor level) 간의 차이에의해서 발생하는 변동과 그 밖의 요인에 의해서 발생하는 변동으로 나누어서 자료를 분석하는 것이 기본원리
기본원리 1,2,와 같이 측정된 값에서 각각의 평균을 뺀 후에
제곱하여 더한다.

<분산북석표>
분산분석표의 제일 오른쪽에 있는 F0 통계량을 이용해서 전체 수준들간의 평균이 같은지 아니면 다른지 검정한다. 기본 개념은, F0 통계량은 처리평균제곱(MSTR)의 크기에 영향을 받는다.
처리평균제곱(MSTR)이 커지면 오차평균제곱(MSE)은 작아지게 되며, 따라서 F0통계량은 분자가 커지고 분모가 작아지기 때문에 당연히 커지게 된다. 즉, F0통계량 값이 크다는 것은 수준평균들간에 평균의 차이가 크다는 의미이다.


위 결과표를 보면 f값이 108.8이고 p-value가 1.2e-13이기 때문에 대립가설1을 채택할 수 있다.
예시 )
attach(mydata)
res<- mytable(BMI_gr ~ sbp1,data=mydata, method=1, digits=1, max.ylev = 5)
res
install.packages("car")
# car는 등분산 검정을 하기 위해서 package를 설치
library(car)
mydata$SRH <-as.factor(mydata$SRH)
# levene test를 실시하기 위해서는 변수 형태를 factor로 변경해야만 한다.
leveneTest(sbp1~BMI_gr, data=mydata) # 등분산성 검정
# mydata 안의 BMRI_gr의 그룹으로 나누어진 sbp1 의 값을 등분산 검정을 진행한다.
result.anova <- aov(sbp1 ~ BMI_gr, data=mydata)
# ANOVA 분석을 진행하는aov 함수를 사용한다.
summary(result.anova) # 분산분석결과 출력
post_hoc.tukey<-TukeyHSD(result.anova,"BMI_gr",ordered=TRUE)
post_hoc.tukey # Tukey방법에 의한 사후검정
plot(post_hoc.tukey)
detach(mydata)
#
결과
Levene's Test for Homogeneity of Variance (center = median)
Df F value Pr(>F)
group 2 1.0627 0.3466
Df Sum Sq Mean Sq F value Pr(>F)
BMI_gr 2 605 302.7 1.8 0.167
Residuals 358 60194 168.1
diff lwr upr p adj
정상-저체중 6.363946 -6.470471 19.198363 0.4737192
과체중-저체중 8.251621 -4.351666 20.854908 0.2730891
과체중-정상 1.887676 -1.735444 5.510796 0.4384698
levene's test는 p-value가 0.3이기 때문에 분산에서 차이가 없다. 다음통계분석을 진행해도 된다.
정상-과체중의 차이는 6.36이고 유의수준에서는 0.47이기 때문에 차이가 없었다. 가 답니다.


댓글
댓글 쓰기